[Medium] CF2026F Bermart Ice Cream

xiezheyuan2025/1/29约 1618 字大约 8 分钟

简要题意

你需要维护一些冰淇淋店，初始时只有一家店，编号为 $1$ ，不出售任何冰淇淋。有 $n$ 次操作，支持：

1 x 开一家新冰淇淋店，分配一个最小的没有分配过的正整数为编号，销售的冰淇淋与此时 $x$ 销售的冰淇淋相同。
2 x p t 冰淇淋店 $x$ 开始出售一种价格为 $p$ 元美味度为 $t$ 的冰淇淋。
3 x 冰淇淋店 $x$ 停止销售最早开始销售的冰淇淋。
4 x p 询问在冰淇淋店 $x$ 花费至多 $p$ 元购买冰淇淋（每种冰淇淋至多买一个），最大的冰淇淋美味度总和。

$1\leq n\leq 3\times 10^4,1\leq p,t\leq 2\times 10^3$ ，保证操作合法。

思路

Part 1

首先不妨离线，将每种操作都挂到冰淇淋店上，然后可以从店 $1$ 开始遍历，如果遇到了 $1$ 操作，就递归（因为此时正好保存了此时这个冰淇淋店出售的冰淇淋状态，可以实现类似可持久化的效果），否则处理对应的操作，最后撤销本次进行的操作（可以直接反向操作）。这个算法不妨称为操作树分治。

然后观察我们如何进行操作，不妨将冰淇淋按照开始出售的时间排序，那么我们始终只会在这个冰淇淋序列的首尾进行插入删除操作，而查询其实可以看成 $01$ 背包，于是我们需要维护一个维护物品双端队列，支持首尾增删和查询此时双端队列的所有物品的 $01$ 背包的结果。

使用线段树分治，可以做到 $O(pn\log n)$ 足以通过本题，不过不是最优的。关于本做法，可以参考 CF601E A Museum Robbery。

Part 2

我们讲一下另一个做法：对顶栈（Minimum / Maximum Deque），因为这个算法通常用于维护双端队列的最值而得名。

为了引入这个算法，先来考虑一个经典问题：

你需要维护一个双端队列，支持首尾增删、查询整个队列的最小值。要求所有操作时间复杂度 $O(1)$ 。

我们发现如果将双端队列换成栈，问题是极为容易的，单独维护一个栈表示前缀最小值即可。我们称这个数据结构为最值栈（Minimum / Maximum Stack）。

这启发我们用栈模拟双端队列。我们将双端队列分成两个栈，两端是栈顶，中间是栈底。，如图所示：

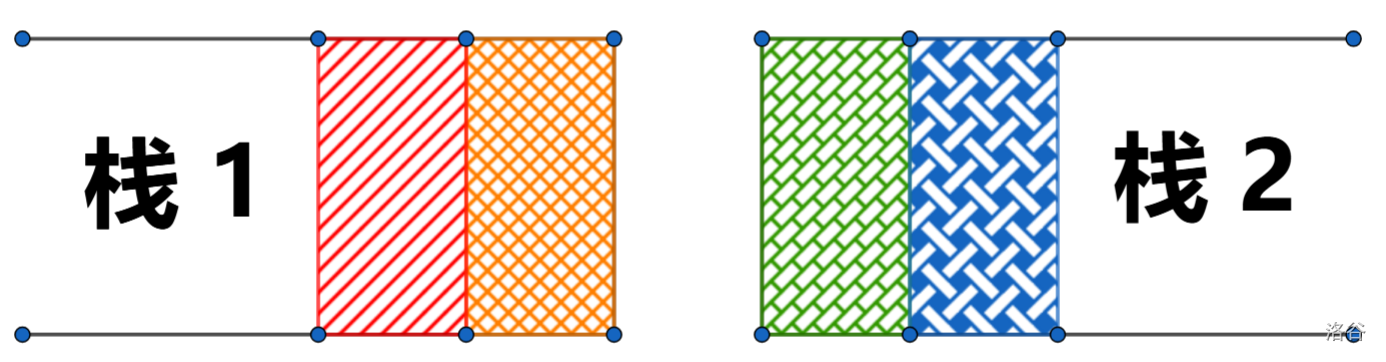
于是首尾插入操作就很好完成了，直接用最值栈模拟即可。查询也是容易的，取两个最值栈的答案的最小值即可。

对于首尾删除操作，如果删除完后，每个栈都是非空的，那么也是容易的，直接套用最值栈的删除即可，关键是如果有一个栈被删空了，我们应该如何处理？

这时我们引入重构（Rebalance）操作，用于将剩下的存在元素的栈，将一半（向上取整）的元素分给另一个空栈，如下图所示：

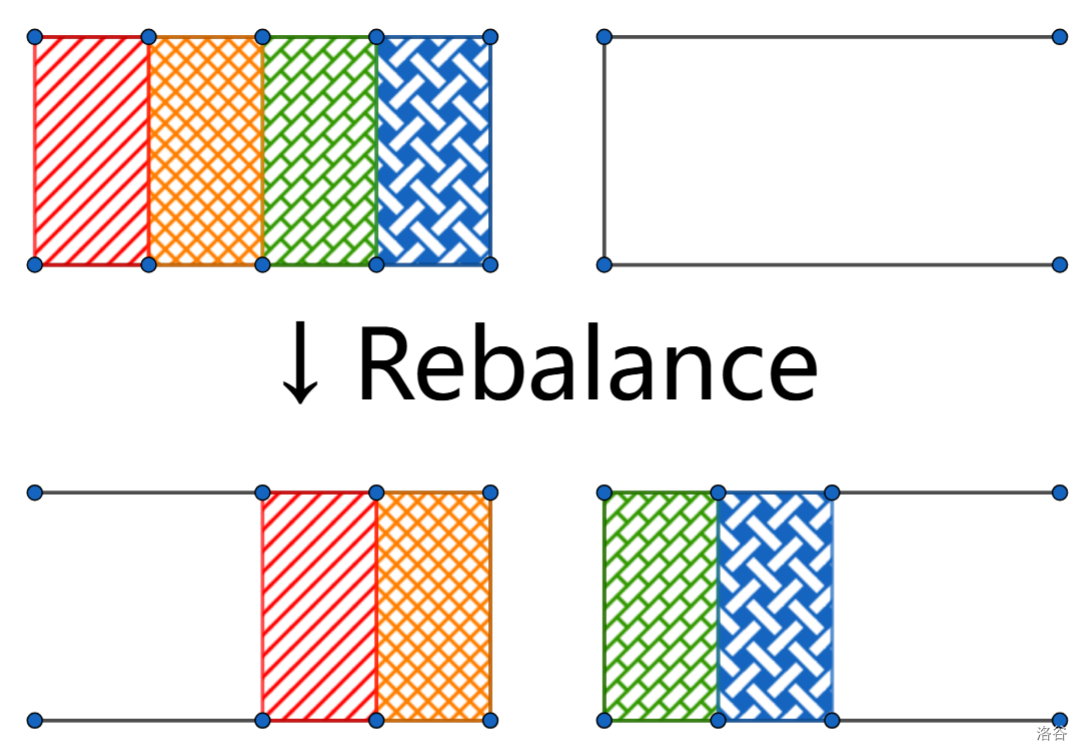
至于重构的实现，可以直接暴力将所有元素提取出来，然后进行分配，方法很多，不再赘述。

这样，我们就可以在栈删空时进行一次重构，这样就可以继续完成接下来的操作了。

使用势能分析法，容易证明所有操作均摊 $O(1)$ ，事实上 STL 中的 std::deque 就使用了类似的维护方法，使用两个栈（std::vector 而不是 std::stack）来实现双端队列的效果。

Part 3

通过 Part 2 的铺垫，我们很容易的将对顶栈技术应用到本题，只需要一个物品栈，支持尾部插入删除，查询整个栈的 $01$ 背包，由于本题是求最大值而不是计数，因此无法使用传统的可撤销背包，不过我们可以维护前缀的 dp 数组来变相的实现可撤销（如果你学习过线段树分治，可能会觉得很熟悉，我们只是省略了每个位置的记录更改过程）。这样插入只需要进行一次背包 dp，删除只需要弹栈。

最后一个问题是如何将两个栈的背包信息合并，这同样是容易的，枚举第一个栈的最大总重量即可。

于是我们借助对顶栈出色地完成了本题，时间复杂度 $O(pn)$ 。

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 3e4 + 5;
int m;

struct min_stack{
    stack<pair<int,int>> s;
    stack<vector<int>> f;
    min_stack(){
        vector<int> h; h.resize(2001);
        f.push(h);
    }
    void push(pair<int,int> val){
        auto [w, v] = val;
        vector<int> h; h.resize(2001);
        vector<int> &g = f.top();
        copy(g.begin(), g.begin() + w, h.begin());
        for(int i=w;i<=2000;i++) h[i] = max(g[i], g[i - w] + v);
        f.push(h), s.push(val);
    }
    void pop(){ s.pop(), f.pop(); }
    bool empty(){ return s.empty(); }
    int size(){ return s.size(); }
    pair<int,int> top(){ return s.top(); }
    int operator[](int x){ return f.top()[x]; }
    void reverse(){
        queue<pair<int,int>> t;
        while(!s.empty()) t.push(s.top()), pop();
        while(!t.empty()) push(t.front()), t.pop();
    }
};

struct min_queue{
    min_stack s[2];
    void push(bool x, pair<int,int> v){ s[x].push(v); }
    void fix(bool x){
        if(!s[x].empty()) return;
        int cnt = s[!x].size() >> 1;
        while(cnt--) s[x].push(s[!x].top()), s[!x].pop();
        s[x].reverse(), s[!x].reverse();
        swap(s[0], s[1]);
    }
    pair<int,int> top(bool x){ return fix(x), s[x].top(); }
    void pop(bool x){ fix(x), s[x].pop(); }
    int query(int x){
        int ans = 0;
        for(int i=0;i<=x;i++) ans = max(ans, s[0][i] + s[1][x - i]);
        return ans;
    }
} mq;

struct option{ int op, x, y; };
vector<option> opts[N];
int answer[N];

void dfs(int u){
    vector<option> tmp;
    for(auto [op, x, y] : opts[u]){
        if(op == 1) dfs(x);
        if(op == 2) mq.push(1, {x, y}), tmp.push_back({3, 0, 0});
        if(op == 3){
            auto [w, v] = mq.top(0);
            tmp.push_back({2, w, v}), mq.pop(0);
        }
        if(op == 4) answer[y] = mq.query(x);
    }
    reverse(tmp.begin(), tmp.end());
    for(auto [op, x, y] : tmp){
        if(op == 2) mq.push(0, {x, y});
        if(op == 3) mq.pop(1);
    }
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> m; int cnt = 1, tot = 0;
    for(int i=1;i<=m;i++){
        int op, x, y, z;
        cin >> op >> x;
        if(op == 1) opts[x].push_back({op, ++cnt, 0});
        if(op == 2) cin >> y >> z, opts[x].push_back({op, y, z});
        if(op == 3) opts[x].push_back({op, 0, 0});
        if(op == 4) cin >> y, opts[x].push_back({op, y, ++tot});
    }
    dfs(1);
    for(int i=1;i<=tot;i++) cout << answer[i] << '\n';
    return 0;
}

// Written by xiezheyuan