2025-07-03 随笔

Minkowski 和与凸优化

在数学上，我们定义两个集合（通常是点集） $S,T$ 的 Minkowsi 和为：

$$S+T=\{x+y|x\in S,y\in T\}$$

OI 一般研究的是满足下述限制的点集：

• 点集的元素的横坐标恰好覆盖区间 $[0, |S|)\cap \mathbb{N}$。
• 点集是一个凸壳，即按照横坐标排序后，相邻两点组成的向量的斜率递增 / 递减。下面我们均讨论斜率递增的情况（即下凸壳）。

不妨考虑两个满足上述性质的点集 $S,T$ 它们的 Minkowski 和。则 Minkowski 和的下凸壳的横坐标为 $k$ 的点的纵坐标一定是：

$$\min_{\substack{(i,x)\in S, (j, y)\in T\\ i+j=k}} x+y$$

或者用更加时髦的说法，$S+T$ 的下凸壳是 $S$ 的下凸壳和 $T$ 的下凸壳的 $(\min, +)$ 卷积。

由于 Minkowski 和本身有 $|S| \cdot |T|$ 个点，这太多了，所以我们一般只研究 $S+T$ 的下凸壳。下文中我们说 $S,T$ 的 Minkowski 和，指的是 Minkowski 和的下凸壳，它的大小只有 $O(|S|+|T|)$。

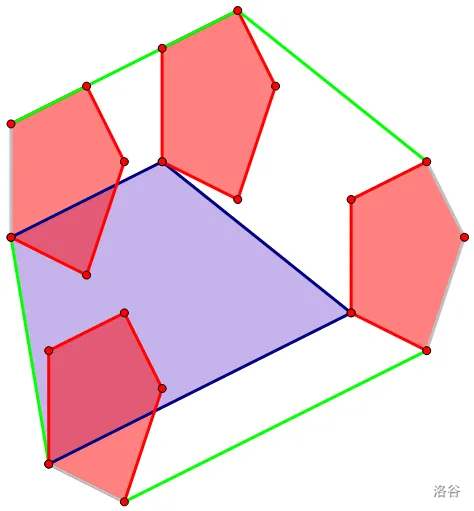
了解了 Minkowski 和的性质，接下来就必须知道它的求法，先上一张经典图：

观察这张图你会发现一个性质：两个凸包的闵可夫斯基和的凸包，每条边的向量都恰好精确覆盖两个凸包的边向量。同理，两个下凸壳的 Minkowski 和的下凸壳，每条边的向量都恰好精确覆盖两个下凸壳的边向量。于是我们只需要求出两个下凸壳的边的斜率，排个序就可以求出 Minkowski 和的下凸壳了。

具体实现的话，注意到我们研究的横坐标总是相邻的整数，因此完全可以用差分数组替代斜率，然后排序。注意由于下凸壳本身斜率就是递增的，将两个递增序列合并成一个递增序列只需要归并即可，最后求前缀和就可以还原。时间复杂度 $O(|S|+|T|)$。

Minkowsi 和的直接用途是，给定两个下凸壳，我们可以快速求出它的 $(\min, +)$ 卷积的结果（结果同样是一个下凸壳）。

来道题：

QOJ6610 Forged in the Barrens：给出一个长度为 $n$ 的序列 $a$，你需要将其分成恰好 $k$ 段，最大化每一段的极差之和。对于每一个 $k\in [1, n]$ 求出这个最大值。

$1\leq n\leq 2\times 10^5$。时间限制 $6\text{s}$，空间限制 $1\text{GB}$。

极差这个东西本身限制很强，在 dp 的过程中记录最值信息比较困难（虽然很容易解决，但是这样你就需要引入 ST 表之类的维护 RMQ 的东西，那就没有优化空间了），不妨继续弱化限制，改成分段后在每一段内选出两个数，最大化它们的差值之和。随后你发现其实这个分段也不重要，只需要选出 $k$ 对数，并且它们不相交且每一对的差值之和最大即可。

那么这样 dp 会简单一点，设设 $f(i, j,0/1/2)$ 表示考虑前缀 $[1,i]$，已经划分成了 $j$ 段，当前没有选不成对的数 / 只选了被减数 / 只选了减数的最大值，转移是分类讨论：

1. 摆烂：$f(i,j,k)\gets f(i-1,j,k)$。
2. 令这个数为被减数：$f(i,j,1)\gets f(i-1,j,0)+a_i,f(i,j,0)\gets f(i-1,j-1,2)+a_i$。
3. 令这个数为减数：$f(i,j,2)\gets f(i-1,j,1)-a_i,f(i,j,0)\gets f(i-1,j-1,2)-a_i$。

这样我们就做到了 $O(n^2)$ 不过难以通过本题。

先来观察这个 dp 函数有什么性质，直接观察它的凸性比较困难，考虑借助一个常见的工具：费用流！

我们发现这个问题如果不在乎时间复杂度的话，那么也可以建立费用流模型，具体地，我们将每个 $a_i$ 拆点，连边 $(L_i,R_i,1,0),(R_i,L_{i+1},\infty,0),(R_i,L_{i-1},\infty,0)$，然后连边 $(S,i,a_i),(i,T,-a_i)$ 表示选择为被减数或者减数，这样没选择一对 $(i,j)$，就必须流过区间 $[i,j]$ 所有形如 $(L_k,R_k,1,0)$ 的边就保证了不交，最后限制总流量 $k$ 即可。那么我们知道费用流的费用函数是凸的，所以答案关于 $k$ 也是凸的。

观察到凸性后，直觉是 wqs 二分，但是 wqs 二分一次只能求出一个点的纵坐标，也就说你要枚举 $k$，每次在二分惩罚过程做一个 $O(n)$ 的 dp，总时间复杂度 $O(n^2\log V)$ 还不如暴力。

不过我们可以发现一个事实（无论你是否承认）：我们每次在做这样一件事情：维护前缀的上凸壳，每次与一个大小为 $2$ 的点集做了一次 Minkowski 和。但是你发现观察到这一点其实没有什么直接的用处，因为 Minkowski 和的时间复杂度为 $O(|S|+|T|)$，虽然 $|T|=2$ 很小，但是 $|S|$ 是逐渐增大到 $n$ 的，直接做与暴力无异。

但是作为卷积，$(\max, +)$ 是有结合律的。回想起一个类似的问题：如何求出若干个二项式的乘积？我们一个一个乘时间复杂度 $O(n^2)$，无论你有没有上 NTT，这是因为没有均衡 $|S|,|T|$，而如果我们分治，$|S|,|T|$ 就会近似相等，时间复杂度就能够最优化，配合 NTT 可以做到 $O(n\log^2 n)$，那么答案似乎已经呼之欲出了。

为了适应分治的形式，我们将 dp 改写为一个区间 dp（因为我好像还没有发现一个类似 GF 的东西来描述这种卷积），设 $f(l,r,k,0/1/2,0/1/2)$ 表示区间 $[l,r]$ 已经凑出了 $k$ 对，以及左边的不完整对的情况和右边的不完整对的情况，取区间内任意一点 $m$，转移又是是分类讨论：

• 抛弃掉其中一个区间的劳动成果：$f(l,r,k,s_1,s_2)\gets \max(f(l,m,k,s_1,s_2), f(m+1,r,k,s_1,s_2))$。
• 左右侧区间的中间都是完整的：$f(l,r,k,s_1,s_2)\gets \max_{x+y=k} f(l,m,x,s_1,0)+f(m+1,r,y,0,s_2)$。
• 左右侧区间的中间是不完整的，并且左侧选择的是被减数：$f(l,r,k,s_1,s_2)\gets \max_{x+y+1=k} f(l,m,x,s_1,1)+f(m+1,r,y,2,s_2)$。
• 左右侧区间的中间是不完整的，并且右侧选择的是减数：$f(l,r,k,s_1,s_2)\gets \max_{x+y+1=k} f(l,m,x,2,s_1)+f(m+1,r,y,1,s_2)$。

这样 $(\max,+)$ 卷积的结构就非常明显，我们可以在分治的时候做三次 $(\max,+)$ 卷积来合并答案即可。时间复杂度 $O(n\log n)$。

您中奖了，再来一题：

QOJ5421 Factories Once More：给定一个 $n$ 个点的树，边有边权，你需要选出恰好 $k$ 个点，使得这些点两两之间的距离之和最大，求这个最大值。$1\leq n\leq 2\times 10^5$，边权 $w\in [1, 10^9]$。

首先有一个暴力的树形 dp，设 $f(u,i)$ 表示点 $u$ 为根的子树，选择了 $k$ 个点的最大两两距离和最大值。转移可以枚举一个儿子 $v$：

$$f(u,i)\gets \max_{x+y=i} f(u,x)+f(v,y)+w(u,v) y (k - y)$$

时间复杂度 $O(n^2)$ 难以通过本题。

$f(y)=w(u,v)y(k-y)=-w(u,v) y^2+w(u,v) ky$ 是一个二次函数，并且是上凸的（二次项系数为负），这很重要，因为若干个凸函数相加和取 $(\max, +)$ 卷积后仍然是凸函数，那么再次考虑用 Minkowski 和来优化。

考虑每个点只维护 dp 的差分数组，这很有道理，因为我们只需要求最后的答案，在根节点求前缀和即可，而合并子树的所有差分数组可以用方便保持有序的结构比如可并堆或者平衡树，及时做垃圾回收的话可以做到空间 $O(n)$。现在的问题是如何给 $f(v,)$ 加上这个二次函数。

为了给 dp 数组加上一个二次函数，不妨考察它对差分数组的变化。我们有 $f(y)-f(y-1) = -w(u,v) (2y-1)+w(u,v) k$ 这是一个一次函数。那么我们要支持给全局按顺序加上一次函数，那么这个平衡树也是能做的，类似线段树那样打 lazy tag 即可，由于我们给一个递减的差分数组加上了一个递减的一次函数，所以不会改变顺序，是良构的。

另外你发现平衡树可能会合并值域相交的区间，这样就假了，我们可以保留重儿子的平衡树，将轻儿子的每个元素暴力插到重儿子的平衡树里（所谓树上启发式合并），这样复杂度就对了，是 $O(n\log^2 n)$ 的。

您打算再做一道题：

QOJ7417 Honorable Mention：给定一个长度为 $n$ 的序列 $a$，有 $q$ 次询问，每次询问给出区间 $[l,r]$ 和参数 $k$。你需要从区间 $[l,r]$ 选择恰好 $k$ 个不交子区间，使得它们的总和最大。输出这个最大值。

$1\leq n,q,|a_i|\leq 3.5\times 10^4$，时间限制 $5000\text{ms}$。

这题的 dp 和 Forged in the Barrens 区别不大，求一遍前缀和后几乎是完全一样的（唯一要注意的是这里被减数一定在减数右侧，另外需要注意我们将一个点 $i$ 选择为减数，应该是减去 $a_{i-1}$ 而不是 $a_i$），唯一的区别是这里需要应付多组询问。

注意到这里其实要干一件类似“分治动态化”的事情，每次要从分治树中选择若干个区间作为询问区间，这不就是线段树吗？于是我们要求出线段树上每个点的 dp 数组，然后回答询问的时候像分治一样合并即可。

等一下，合并？你发现如果直接用 Minkowski 和的方法合并，那么时间复杂度和询问区间长度有关（因为线段树拆出的区间长度关系没有任何保证）。

既然不能合并，能不能不合并呢？当然可以！由于此时我们只需要求出一个 $k$ 的值，所以可以 wqs 二分，这样选择区间就没有限制了，只需要加上惩罚，每次从线段树拆出的区间中选择加上惩罚后的最大值即可。这样时间复杂度是多少呢？wqs 二分 $O(\log V)$，拆出了 $O(\log n)$ 个区间，在每个区间上你需要计算加权最大值，这个可以用二分实现，这需要 $O(\log n)$ 的时间。所以总时间复杂度 $O(q\log^2 n\log V)$，可以通过但是比较卡常。