[Medium] CF1841F Monocarp and a Strategic Game

xiezheyuan2025/2/12约 1067 字大约 5 分钟

简要题意

你在玩一种游戏，角色有四种类型，分别为 $A,B,C,D$ ， $A,B$ 互相敌对， $C,D$ 互相敌对。

有 $n$ 个需求，第 $i$ 个需求表示为四元组 $(a,b,c,d)$ ，这意味着有每个类型分别有给定数量的人希望入住。定义每个角色的收益，为与其同类型的角色数（不包括自己）减去与其敌对的角色数。定义你的收益为所有角色的收益总和加上入住的角色数。

你需要选取任意个需求并满足，使得你的收益尽可能大，输出这个最大值。

$1\leq n\leq 3\times 10^5$ 。

思路

Part 1

考虑最后每个类型分别有 $A,B,C,D$ 个角色入住，则收益为：

\begin{aligned} &A(A-1)+B(B-1)+C(C-1)+D(D-1)-2AB-2CD+(A+B+C+D)\\ =&A^2+B^2+C^2+D^2-2AB-2CD\\ =&(A-B)^2+(C-D)^2\\ =&|(A-B,C-D)|^2 \end{aligned}

最后可以得到一个类似点到点的距离的形式，我们不妨写成向量模长的形式。由于向量加法就是每一维相加，于是自然而然可以用向量去描述游戏的操作。对于每一个入住需求，可以表示成 $(a-b,c-d)$ ，转换为下面的问题：

有 $n$ 个向量，你需要选出若干个向量，使得它们的和的模长最大，输出这个最大值。

Part 2

先来观察一下有若干个向量，模长最大的那一个有什么性质。首先向量可以只保留终点，那么就变成研究点集。平面点集的研究方法很有限，我们很容易想到，模长最大的向量的终点一定在所有终点的凸包上。根据凸包的性质，这也是容易理解的。

于是我们想维护所有子集的向量和的终点的凸包（这有一个时髦的概念：闵可夫斯基和）。不过我们不妨画出凸包的形状：

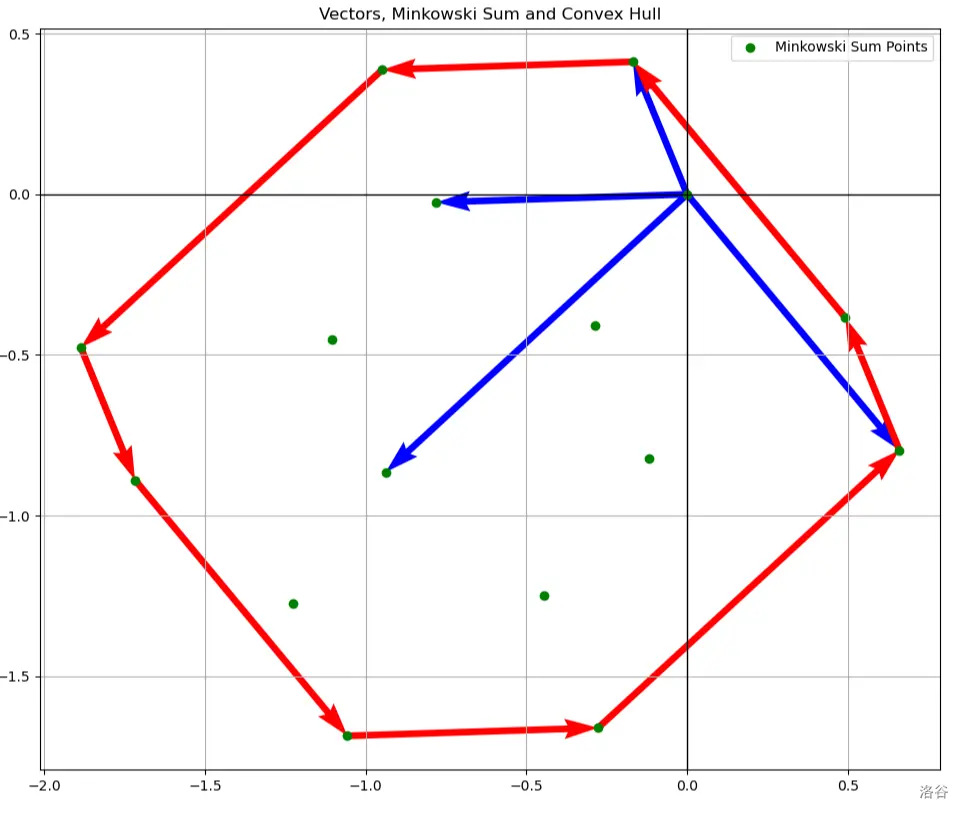
图中，红色的向量表示凸包相邻之间构成的向量，绿色的点表示所有子集得到的向量和的终点，蓝色的向量表示初始的向量集合中的向量。

仔细观察上图，可以发现凸包上的所有边都是与初始向量集平行的，进一步发现凸包上的向量，是由初始向量和其相反向量构成的。在此，我们不加证明地给出这个结论，至于证明请参考扶苏的题解。

于是凸包边只有 $2n$ 条，并且向量是已知的。我们先对这些向量极角排序，方便构建这个凸包，以期枚举凸包上的点来统计答案。

Part 3

如果我们确定了凸包上的一个点，就可以还原出凸包了，现在我们需要找到一个点。

注意到正常的极角排序是从斜率为负的向量开始，所以最开始的一条边就是上凸壳最左侧的边，于是我们可以将所有 $x$ 为负数的点累加即可，注意如果为 $0$ ，我们希望在 $y$ 轴下。

时间复杂度 $O(n\log n)$ 。

代码

#include <bits/stdc++.h>
#pragma GCC optimize("Ofast", "inline", "-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
using namespace std;

using i128 = __int128;
using i64 = long long;
const int N = 3e5 + 5;
tuple<int,int,double> p[N << 1];
int n;

i128 hypt(i64 x, i64 y){ return (i128)x * x + (i128)y * y; }

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n;
    i64 x = 0, y = 0;
    for(int i=1,a,b,c,d;i<=n;i++){
        cin >> a >> b >> c >> d;
        p[(i << 1) - 1] = {a - b, c - d, atan2(a - b, c - d)};
        p[i << 1] = {b - a, d - c, atan2(b - a, d - c)};
        if(a - b > 0 || (a == b && c < d)) x += a - b, y += c - d;
    }
    sort(p + 1, p + (n << 1) + 1, [](auto a, auto b){
        return get<2>(a) < get<2>(b);
    });
    i128 ans = hypt(x, y);
    for(int i=1;i<=(n<<1);i++){
        x += get<0>(p[i]), y += get<1>(p[i]);
        ans = max(ans, hypt(x, y));
    }
    string s;
    if(!ans) s = "0";
    while(ans) s += (ans % 10) + '0', ans /= 10;
    reverse(s.begin(), s.end());
    cout << s << '\n';
    return 0;
}

// Written by xiezheyuan