Slope Trick 优化 DP

xiezheyuan2025/6/2约 1063 字大约 5 分钟

消歧义

本文讲述的不是斜率优化（Convex Hull Trick）而是 Slope Trick。

Slope Trick 基础

斜率表示法

Slope Trick（无标准译名，与斜率优化不同）通常用于优化一类二维 dp，满足：

对于二维 dp 的每一行，都可以看成关于列的一个函数，并且它具有凹性或凸性。
每一行的函数，都可以看成是一个连续的分段函数，每一段是一个一次函数。

通常这样的函数是难以刻画的，我们有一个较好的方法：斜率表示法，它的规则如下：

通过其他方法记录最左边或最右边的一次函数的斜率和截距。
记录每一个段与段之间交点的横坐标，如果第一段的斜率为 $k_1$ ，第二段的斜率为 $k_2$ ，就记录 $|k_1-k_2|$ 次。

例如下面的分段函数：

\begin{cases} 5-2 x & x\leq 1 \\ 4-x & 1<x\leq 2 \\ x & x>2 \\ \end{cases}

可以绘图如下：

根据上面的约定的方法，我们可以将分段函数记录为 $\{1,2,2\}$ 。

凹凸函数的形式化定义

这里将给出凹凸函数的形式化定义，方便我们之后的分析。

定义

对于函数 $f$ ，若对于任意的 $x,y$ 和 $\lambda\in[0,1]$ 均有：

f(\lambda x + (1 - \lambda) y) \geq \lambda f(x) + (1 - \lambda) f(y)

则称 $f$ 为凹函数。若满足：

f(\lambda x + (1 - \lambda) y) \leq \lambda f(x) + (1 - \lambda) f(y)

则称 $f$ 为凸函数。

此外若 $f$ 一阶可导，则还有另一个实用的定义是： $f$ 的导数不减则为凸函数， $f$ 的导数递增则为凹函数。

下面的讨论中我们都是用凹函数，凸函数是类似的。

函数的加减法

例如考虑两个分段函数：

\begin{aligned} &F(x)=\begin{cases} 5-2 x & x\leq 1 \\ 4-x & 1<x\leq 2 \\ x & x>2 \\ \end{cases}\\ &G(x)=\begin{cases} 3-x & x\leq 1 \\ 2 & 1<x\leq 3 \\ x-1 & x>3 \\ \end{cases} \end{aligned}

我们不妨先绘制出 $F(x),G(x),F(x)+G(x),F(x)-G(x)$ 的图表：

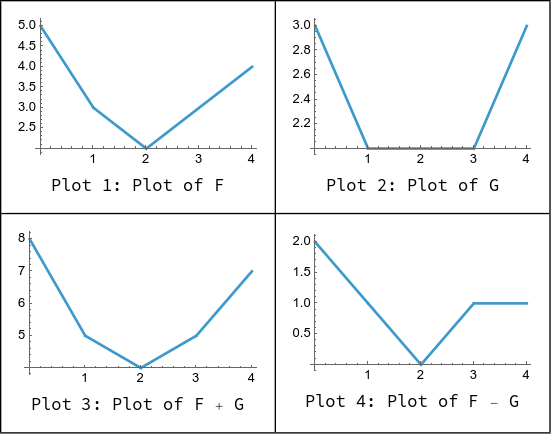
可以发现 $F(x)+G(x)$ 仍然保持了 $F(x),G(x)$ 的凹性，但是 $F(x)-G(x)$ 不一定会保持。

定理

若 $F(x),G(x)$ 均是凹函数，则 $F(x)+G(x)$ 亦是凹函数。

证明：

\begin{aligned} F(\lambda x + (1 - \lambda) y)+G(\lambda x + (1 - \lambda) y) &\geq F(x) + (1 - \lambda) F(y) + G(x) + (1 - \lambda) G(y)\\ &=(F(x)+G(x))+(1-\lambda)(F(y)+G(y))\quad\Box\\ \end{aligned}

接下来考虑两个凹函数加起来后，它的斜率表示是什么。可以发现应当是两个凹函数的的斜率表示的并。

前缀最小值 / 后缀最大值

考虑下面的函数：

F(x)=\begin{cases} 8-3 x & x\leq 1 \\ 6-x & 1<x\leq 2 \\ x+2 & 2<x\leq 3 \\ 2 x-1 & x>3 \\ \end{cases}

我们绘制它的前缀最小值函数 $\min\limits_{k=0}^{x}F(k)$ 以及后缀最大值函数 $\min\limits_{k=x}^{4}F(k)$ 。

可以发现 $F$ 的前缀最小值和后缀最大值都是凹的（很容易想到后缀最小值和前缀最大值不一定满足该性质）。

定理

若 $F$ 为凹函数，则任取一个 $k$ ，有：

$G(x)$ 定义为 $F$ 在 $[k,x]$ 的最小值，则 $G$ 定义域为 $[k,\infty)$ ， $G$ 同样为凹函数
$G(x)$ 定义为 $F$ 在 $[x,k]$ 的最大值，则 $G$ 定义域为 $(-\infty,k]$ ， $G$ 同样为凹函数。

凸函数间的最值

考虑下面两个函数：

\begin{aligned} &F(x) = \begin{cases} 6-5x & x \le 1 \\ 1 & 1 < x \le 3 \\ -11+4x & x > 3 \end{cases}\\ &G(x) = \begin{cases} 4-x & x \le 1 \\ 3 & 1 < x \le 2 \\ -7+5x & x > 2 \end{cases} \end{aligned}

我们绘制 $F(x),G(x),\min(F(x),G(x)),\max(F(x),G(x))$ 的函数图像：

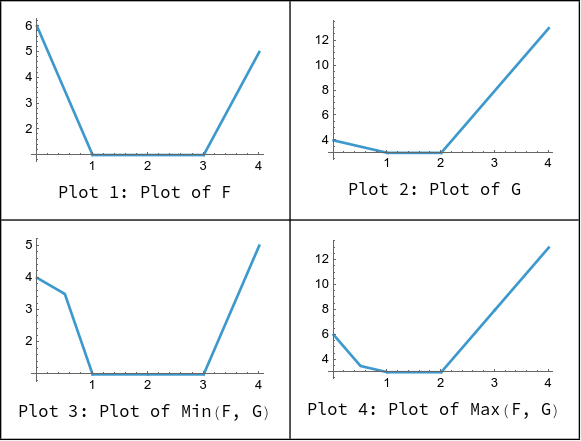
可以发现 $\min(F(x),G(x))$ 不是凹函数， $\max(F(x),G(x))$ 为凹函数。

（事实上当 $F(x),G(x)$ 为凸函数时上述规律仍然成立）

我们可以给出以下定理：

定理

若 $F(x),G(x)$ 为凹函数，则 $\max(F(x),G(x))$ 亦为凹函数。