定义

我们定义一个数 $n$ 在模 $p$ 意义下是二次剩余，当且仅当 $\exist x\neq 0, x^2\equiv n\pmod{p}$。

例如 $p=23$ 时有 $11$ 个数是二次剩余，分别为 ${1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18}$。

有一个基本的观察，这个同余方程只会有两个解 $x_1,x_2$，并且 $x_1=-x_2$，证明是平凡的。

Legendre 符号

定义 Legendre 符号表示：

$$\left(\frac{n}{p}\right)=\begin{cases} 0& p\mid n\\ 1& \exist x\neq 0, x^2\equiv n\pmod{p}\\ -1& \text{otherwise} \end{cases}$$

下面是 Wikipedia 上给出的 Legendre 符号表：

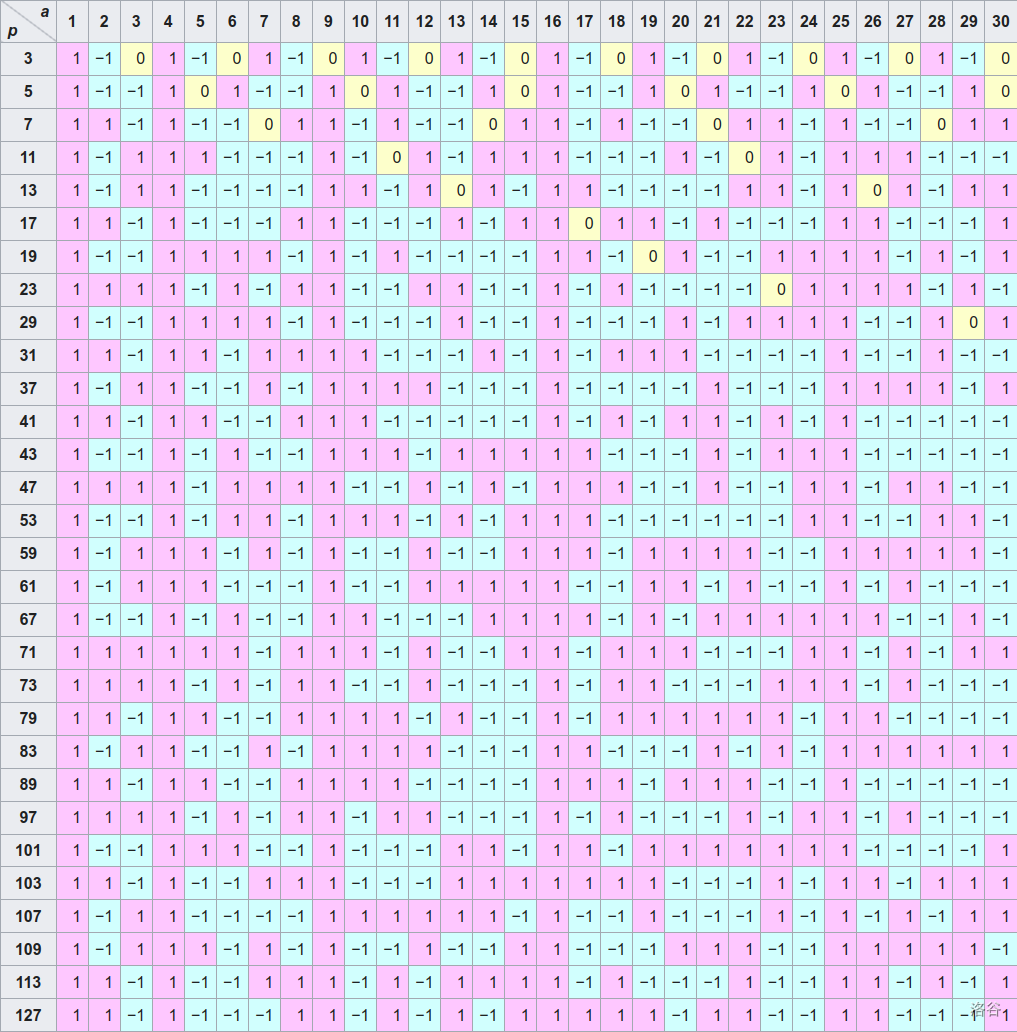
Euler 准则

定理（Euler's Criterion）：对于奇素数 $p$ 和一个整数 $n$，有：

$$\left(\frac{n}{p}\right)\equiv n^{(p-1)/2}\pmod{p}$$

也就是说，若 $n^{(p-1)/2}\equiv 1\pmod{p}$，那么 $n$ 是一个模 $p$ 意义下的二次剩余。

证明

若 $n,p$ 不互质，则必有 $p\mid n$，进而 $p\mid n^{(p-1)/2}$。故 $n^{(p-1)/2}\equiv 0\pmod{p}$ 符合 Euler 准则。故下面只考虑 $\gcd(n,p)$ 的情况。

首先根据费马小定理，有 $n^{p-1}\equiv 1\pmod{p}$，故 $(n^{(p-1)/2})^2\equiv 1\pmod{p}$。因此 $n^{(p-1)/2} \equiv \pm 1\pmod{p}$。

因此只需要证明 $n^{(p-1)/2}\equiv 1\pmod{p}$ 是 $n$ 为模 $p$ 意义下的二次剩余的充要条件即可。

必要性：

若 $n$ 为模 $p$ 意义下的二次剩余，则任取一个 $x$ 满足 $x^2\equiv n\pmod{p}$。代入并应用费马小定理，得到 $n^{(p-1)/2}\equiv x^{p-1}\equiv 1\pmod{p}$，证毕。

充分性：

根据原根存在定理，可取模 $p$ 意义下的一原根 $g$，则一定存在 $n$ 的以一个离散对数 $k$，即 $g^k\equiv n\pmod{p}$。

代入，得到 $g^{k(p - 1)/2}\equiv n^{(p - 1)/2}\equiv 1\pmod{p}$。

根据费马小定理，得到 $(p-1)\mid \left(\frac{k(p - 1)}{2}\right)$。那么 $\frac{k}{2}\in \mathbb{Z}$，也就是 $k$ 为偶数。

那么取 $x=g^{k/2}$，则可得到 $x^2\equiv n\pmod{p}$。故 $n$ 是模 $p$ 意义下的一个二次剩余，证毕。

Cipolla 算法

Cipolla 算法用于找到同余方程 $x^2\equiv n\pmod{p}$ 的一组解，其中 $p$ 为奇素数。

先利用 Euler 准则判定是否存在解。故下面只讨论有解的情况。

我们任意选择一个 $a$，使得 $a^2-n$ 非二次剩余（可以用 Euler 准则判定）。

那么令 $z^2\equiv a^2-n\pmod{p}$。那么有 $(a+z)^{p+1}\equiv n\pmod{p}$（为什么呢？详见下文【正确性证明】），故 $(a+z)^{(p+1)/2}$ 是一组解。

注意到一定是不存在整数 $z$ 满足条件。不妨扩充数域（可以类比复数域），定义这个数域中的数 $x$ 形如 $a+bz$，其中 $a,b\in \mathbb{Z}/p\mathbb{Z}$。并且类比复数定义乘法即可。

于是你发现这个解虚部总是 $0$，于是便得到了一个解。

正确性证明

容易发现只需要证明 $(a+z)^{p+1}\equiv n\pmod{p}$，即可证明得到的解虚部总为 $0$（因为 $n$ 是模 $p$ 意义下的二次剩余），并且是一组合法的解。

注意到 $(a+z)^{p+1}\equiv (a+z)(a+z)^p\pmod{p}$。

然后我们需要知道一个引理：

$(a+b)^p\equiv a^p+b^p\pmod{p}$

证明：考虑应用二项式定理：

$$(a+b)^p=\sum_{k=0}^p\binom{p}{k}a^kb^{p-k}$$

注意到若 $k\in(0,p)$，则 $p\mid \binom{p}{k}$，故这些项在模 $p$ 意义下都为 $0$，证毕。

于是 $(a+z)^p\equiv a^p+z^p\pmod{p}$。由于费马小定理，有 $a^p\equiv a\pmod{p}$。

对于 $z^p$，有 $z^p\equiv z\cdot z^{p-1}\equiv z\cdot (a^2-n)^{(p-1)/2}\pmod{p}$。

根据 Euler 准则，有 $(a^2-n)^{(p-1)/2}\equiv -1\pmod{p}$，所以 $z^p\equiv -z\pmod{p}$。

因此我们得到 $(a+z)^p\equiv a-z\pmod{p}$。

所以 $(a+z)^{p+1}\equiv (a+z)(a-z)\equiv a^2-z^2\equiv n\pmod{p}$，证毕。

时间复杂度证明

在算法流程中有一行：

我们任意选择一个 $a$，使得 $a^2-n$ 非二次剩余（可以用 Euler 准则判定）。

那么需要证明 $a^2-n$ 非二次剩余的概率。

首先给出一个引理：

对于奇素数 $p$，模 $p$ 意义下的二次剩余共有 $\frac{p-1}{2}$ 个。

证明非常简单。由于形如 $x^2\equiv n\pmod{p}$ 的解有 $2$ 个，并且对于不同的 $n$（$0<n<p$），不会有公共解。所以只需要取遍 $0<x<p$，每两个取出的数会构成一个有解同余方程的所有解，所以一共有 $\frac{p-1}{2}$ 个有解方程，证毕。

那么任意取一个数 $x$，它为模 $p$ 意义下的（非）二次剩余的概率为 $\frac{1}{2}+O(1)$。

因此，可以近似看成每一次选取 $a$，$a^2-n$ 非二次剩余的概率为 $\frac{1}{2}+O(1)$，因此期望 $2$ 次就可以找到合适的 $a$。

所以时间复杂度为 $O(\log p)$，瓶颈在快速幂。

代码实现

下面给出模板题的实现：

#include <bits/stdc++.h>
using namespace std;

struct cipolla_complex {
    int x, y, us, mod;
    cipolla_complex(int _x, int _y, int _us, int _mod): x(_x), y(_y), us(_us), mod(_mod) {}
    cipolla_complex operator*(const cipolla_complex &rhs){
        return cipolla_complex(
            (1ll * x * rhs.x + (1ll * y * rhs.y % mod) * us) % mod,
            (1ll * x * rhs.y + 1ll * y * rhs.x) % mod,
            us, mod
        );
    }
};

cipolla_complex fastpow(cipolla_complex a, int n){
    cipolla_complex res = {1, 0, a.us, a.mod};
    while(n){
        if(n & 1) res = res * a;
        a = a * a, n >>= 1;
    }
    return res;
}

int fastpow(int x, int y, int mod){
    int ret = 1;
    while(y){
        if(y & 1) ret = 1ll * ret * x % mod;
        x = 1ll * x * x % mod, y >>= 1;
    }
    return ret;
}

mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());

int cipolla(int n, int mod){
    if(fastpow(n, (mod - 1) >> 1, mod) != 1) return -1;
    int a, us;
    do {
        a = rnd() % mod, us = ((1ll * a * a + mod) - n) % mod;
    } while(fastpow(us, (mod - 1) >> 1, mod) != mod - 1);
    return fastpow(cipolla_complex(a, 1, us, mod), (mod + 1) >> 1).x;
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int t; cin >> t;
    while(t--){
        int n, mod; cin >> n >> mod;
        if(n == 0) {cout << 0 << '\n'; continue; }
        int ans = cipolla(n, mod);
        if(!(~ans)) cout << "Hola!" << '\n';
        else cout << min(ans, mod - ans) << ' ' << max(ans, mod - ans) << '\n';
    }
    return 0;
}

// Written by xiezheyuan